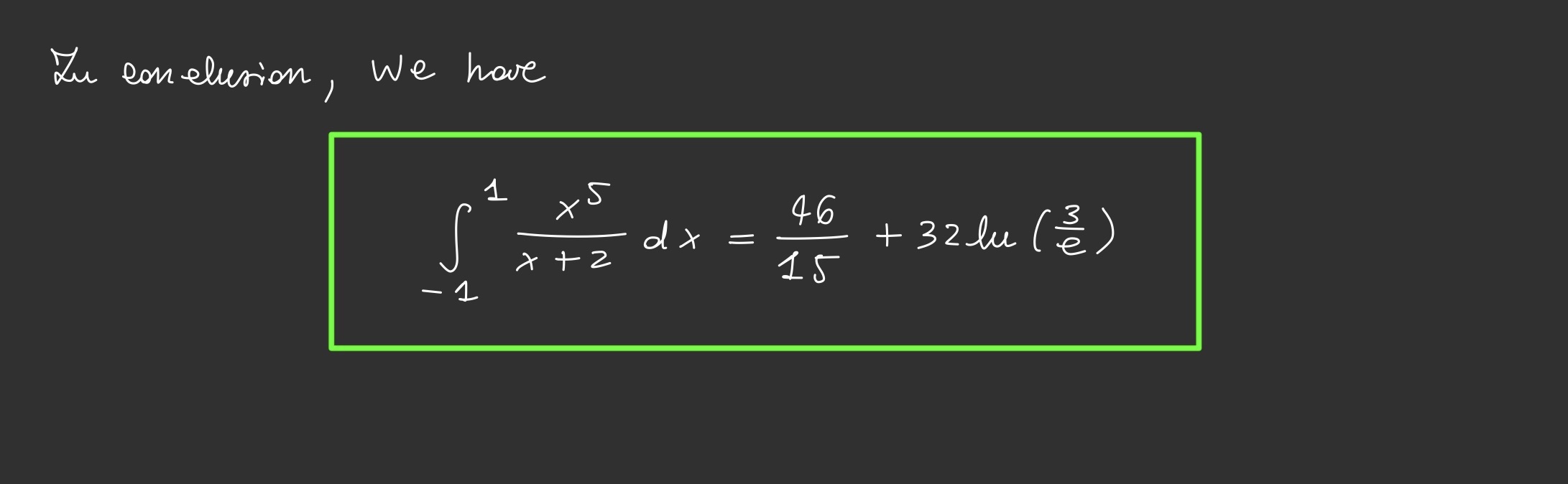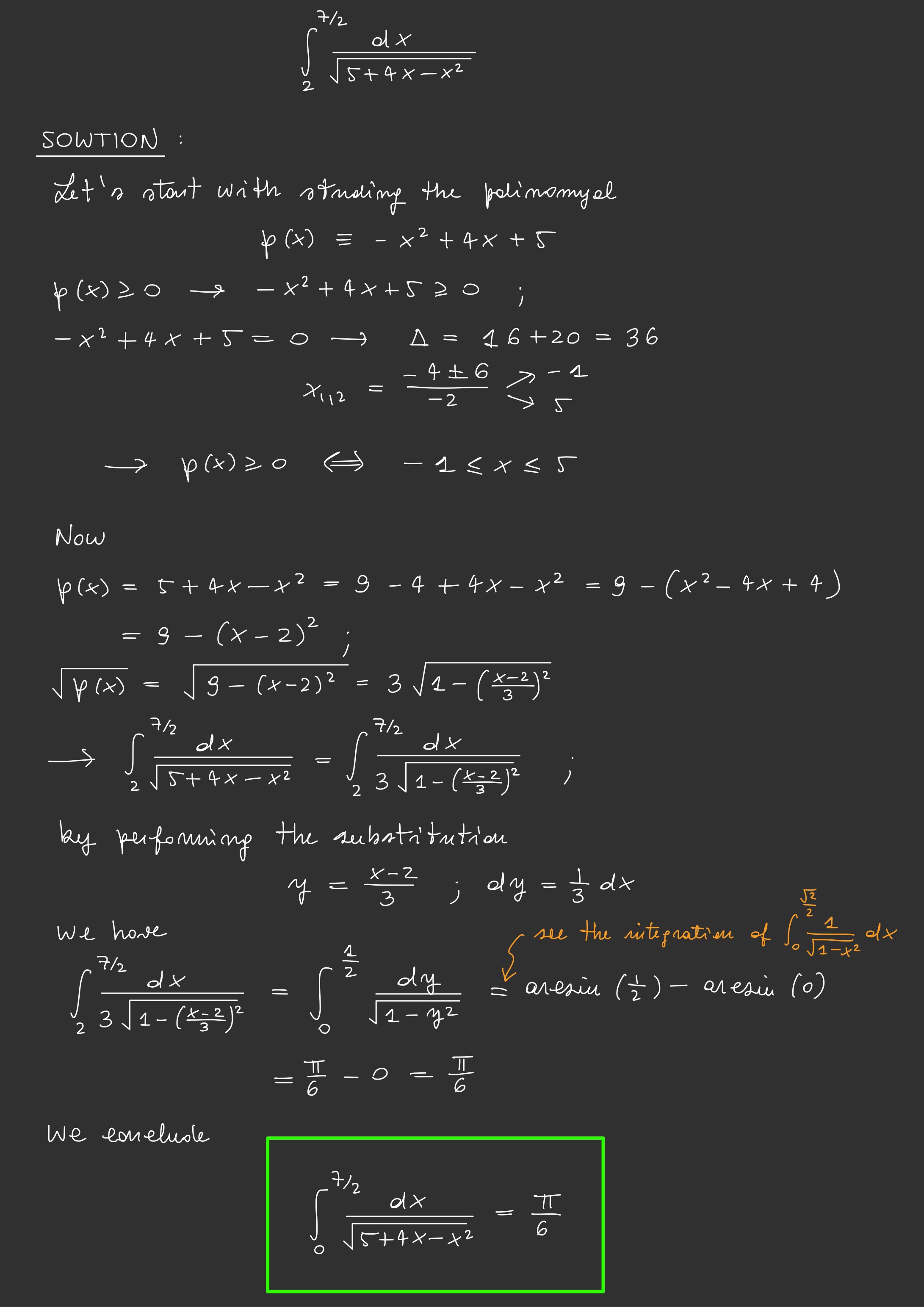A collection of exercises on integrals
Introduction
Welcome to this section dedicated to integrals, a resource
for mastering the art of integrals! Whether you're just
starting out with basic calculus or diving into more
advanced concepts, this collection offers a comprehensive
set of exercises designed to enhance your understanding of
definite and improper integrals.
Integrals are a fundamental concept in calculus, playing a
crucial role in analyzing areas, volumes, and many other
applications across various fields of science and
engineering. This resource breaks down these concepts into
approachable steps, using clear examples and rigorous
definitions to guide you through the journey.
Here, you will find:
- A solid introduction to the Riemann Integral, the cornerstone of understanding definite integrals.
- Challenging exercises to solidify your grasp of improper integrals.
- Step-by-step solutions and explanations that help you not only solve problems but also understand the underlying principles.
Whether you are preparing for exams, honing your skills, or
exploring integral calculus for the love of mathematics,
this platform is designed to make your learning journey
smooth, insightful, and engaging.
This page is constantly growing, with new exercises and
examples being added regularly. If you would like to suggest
new content or report any errors, please feel free to
contact me using the form at the end of the page. Let’s
explore the beautiful world of integrals together!
Definite Integrals
The definition of the Riemann Integral for real function of a real variable
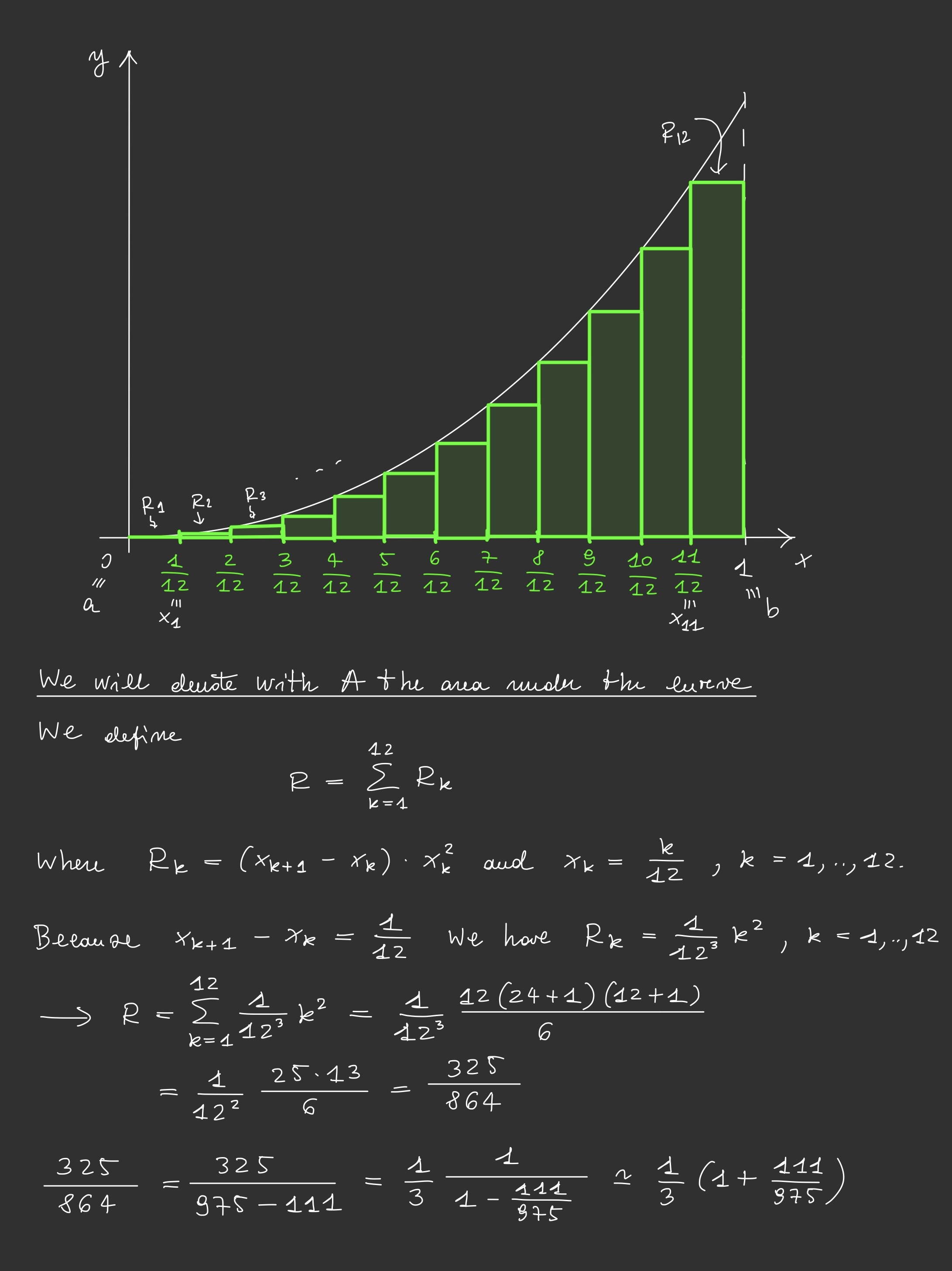
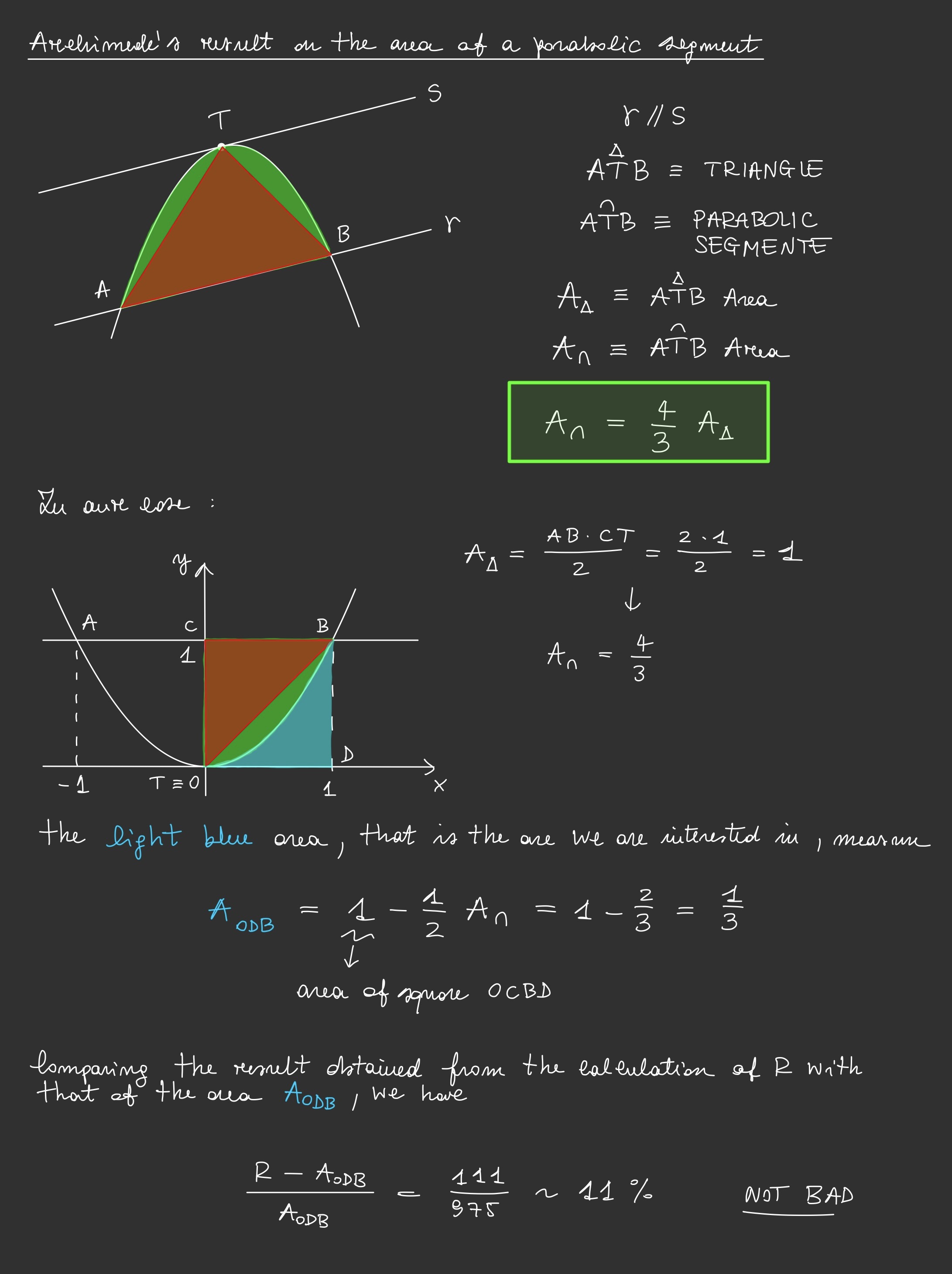
To introduce the Riemann integral, we will heuristically discuss the following example. We aim to calculate the area under the parabola defined by the equation \(y = x^2\) for \(x\) ranging from 0 to 1. Using this example, we will subsequently provide a rigorous definition of the Riemann integral.
This example of calculating the area of the parabolic sector is particularly significant because the great mathematician Archimedes of Syracuse derived a formula for this area. We will compare the result obtained using Riemann's integration method with the result found by Archimedes to confirm the accuracy of our findings in the subsequent steps.
Calculation of the area under the curve \(y = x^2\) for \(x\) ranging from 0 to 1
Before we delve into the details of the calculations, we need to recall the following result.
\[\sum_{k=1}^n k^2 = \frac{n(2n + 1)(n + 1)}{6}\]
Proof of the Formula
This is where you can provide the proof content or any other details.
Keeping this result in mind, we proceed with the calculation of the area.
Exercises on definite integrals
Now that we have heuristically introduced the Riemann integral, let's do some exercises. Below, you will find a list of integrals computed by me. Try solving them yourself first, and only after you have completed your calculations, click on the card of an integral to compare your solution. Have fun with integrals!
\[\int_{0}^1\frac{e^{3x - 1}}{e^{2(3x - 1)} + e^{3x - 1}} \, dx\]
\[\int_{0}^1\frac{x^3}{x^2 + 1} \, dx\]
\[\int_{1}^{e} \ln x \, dx\]
\[\int_{0}^1 xe^{-x^2} \, dx\]
\[\int_{0}^{\pi/2} \sin^2(x) \, dx\]
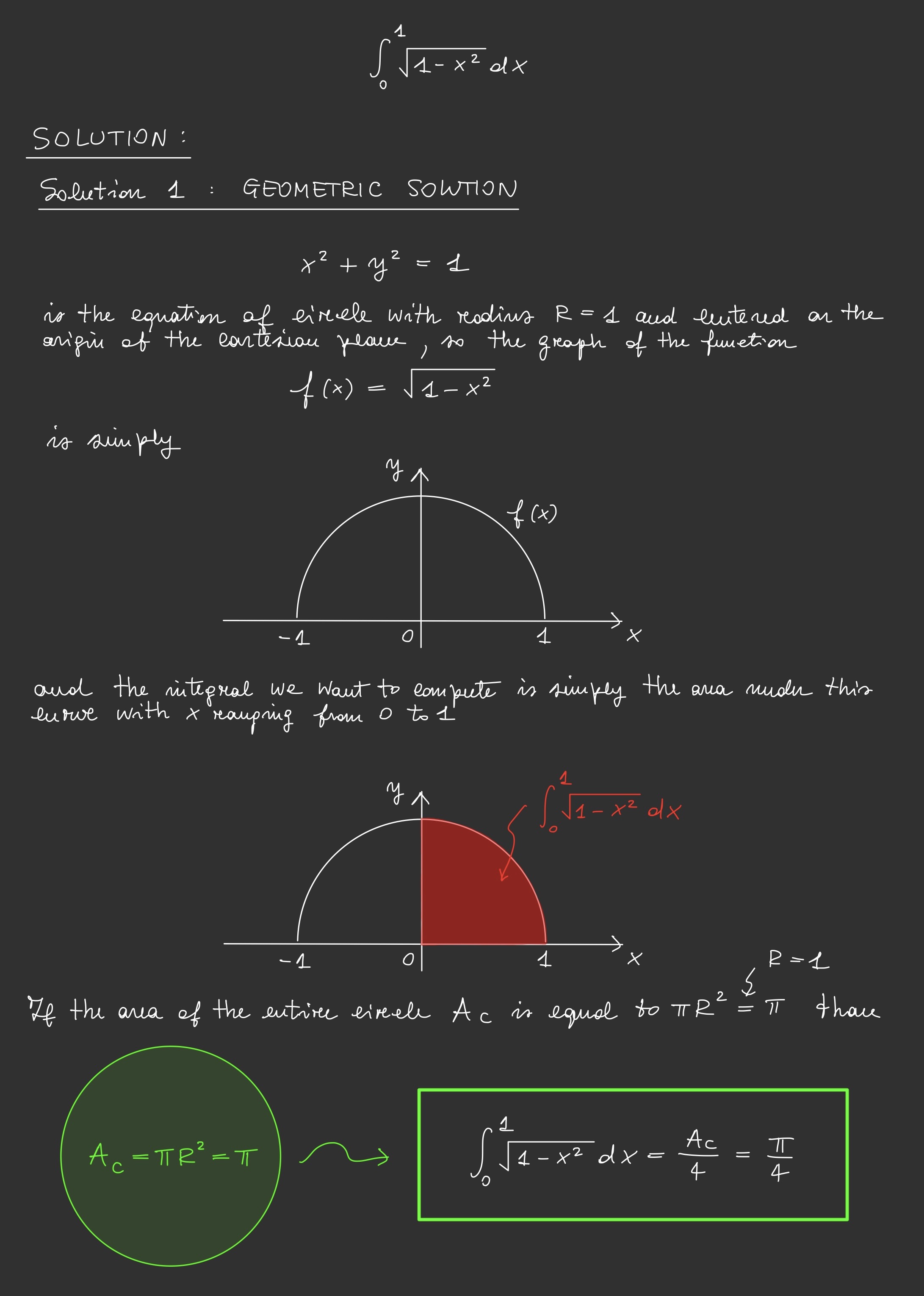
\[\int_{0}^{1} \sqrt{1 - x^2} \, dx\]
\[\int_{-1}^{1} \frac{x^5}{x + 2} \, dx\]
\[\int_{0}^{1} \frac{x^3}{x^8 + 1} \, dx\]
\[\int_{\pi / 6}^{\pi / 4} \frac{1}{\cos^2(x)} \, dx\]
\[\int_{0}^{\sqrt{2} / 2} \frac{1}{\sqrt{1 - x^2}} \, dx\]
\[\int_{2}^{7/2} \frac{1}{\sqrt{5 + 4x - x^2}} \, dx\]
\[\int_{2}^{3} \frac{1}{\sqrt{2^x - 4}} \, dx\]
The next exercise involves solving an indefinite integral, focusing solely on calculating the antiderivative. This integral is deliberately more complex than the previous one to allow for a detailed exploration of various integration techniques. By working through this problem, we’ll delve into the use of hyperbolic functions and substitution methods, illustrating the flexibility and depth of integration.
\[\int \frac{1}{\sqrt{1 + x^2}} \ dx\]
Solution
Solution
Solution
Solution
Solution
Solution
Solution
Solution
Solution
Solution
Solution
Solution
Solution
Improper Integrals
Calculation of improper integrals
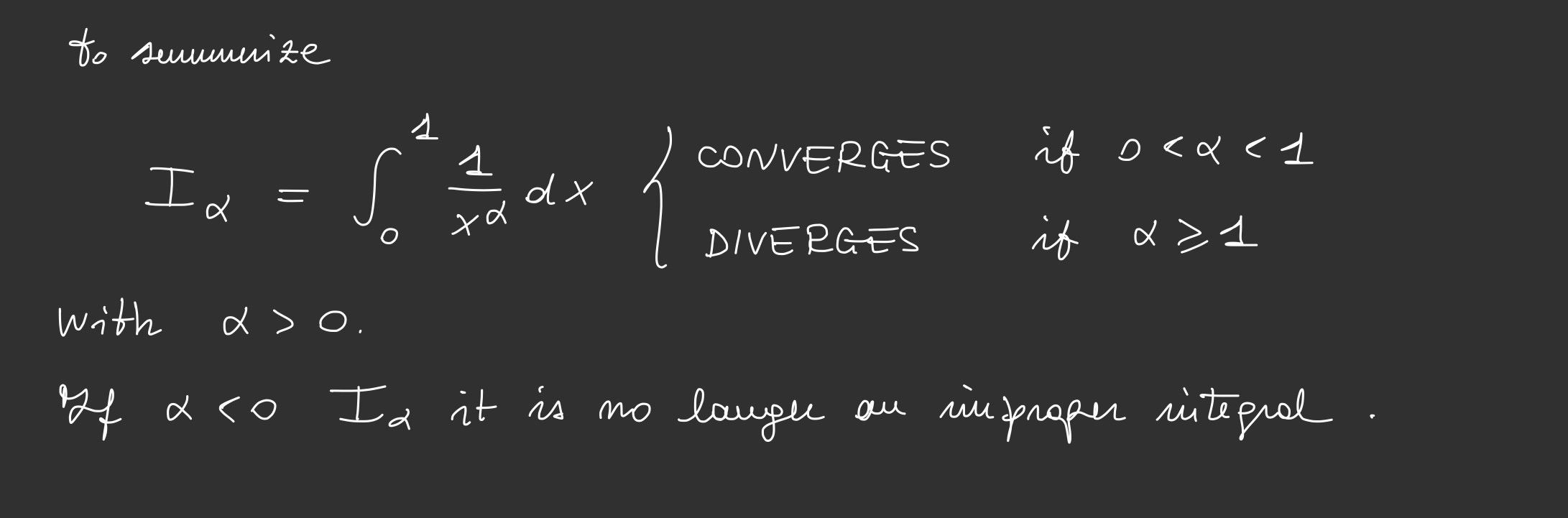
contact
Let's Collaborate!
hello@lupomarco
* Marked fields are required to fill.
